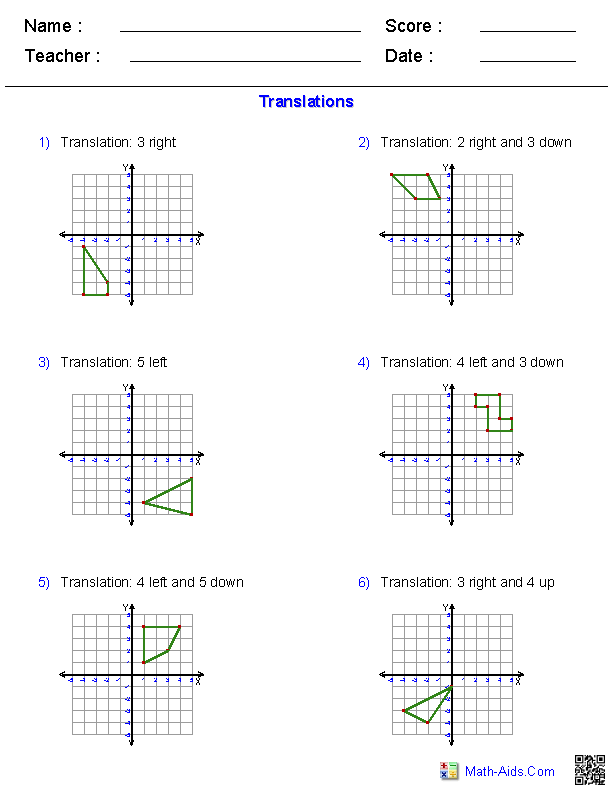
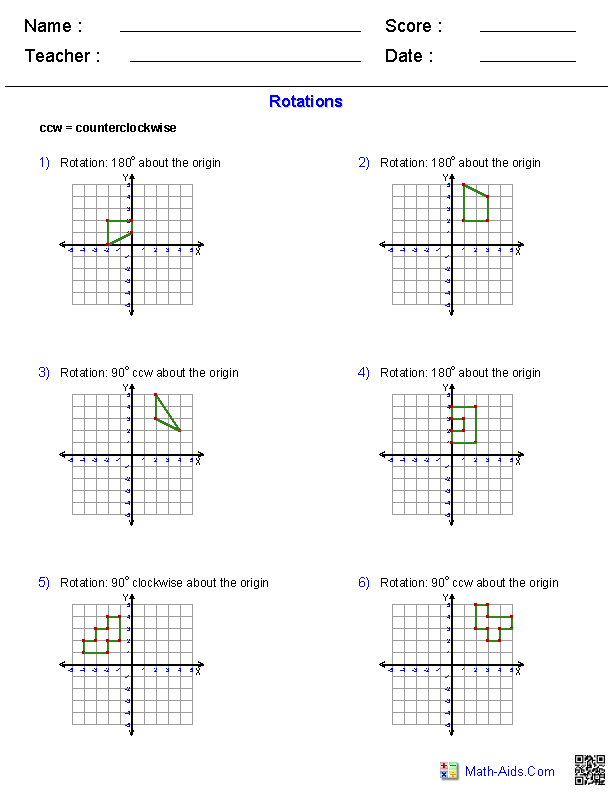
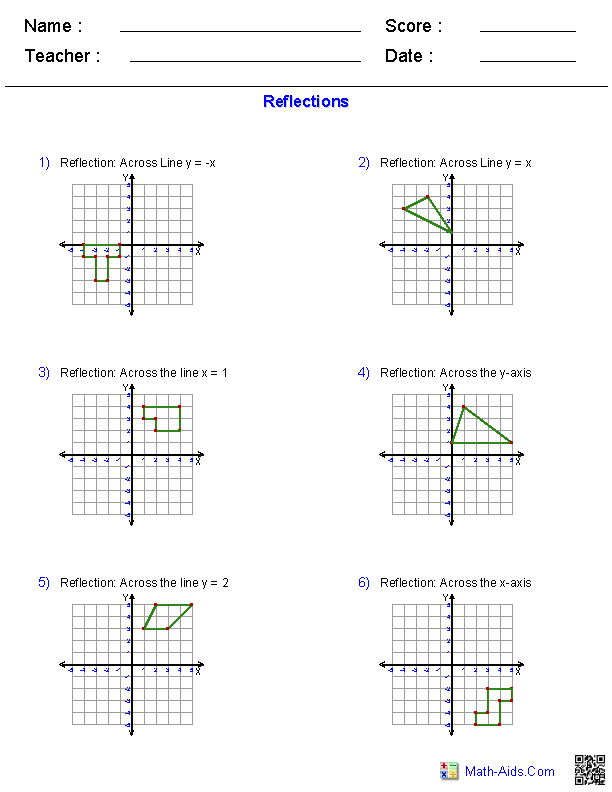
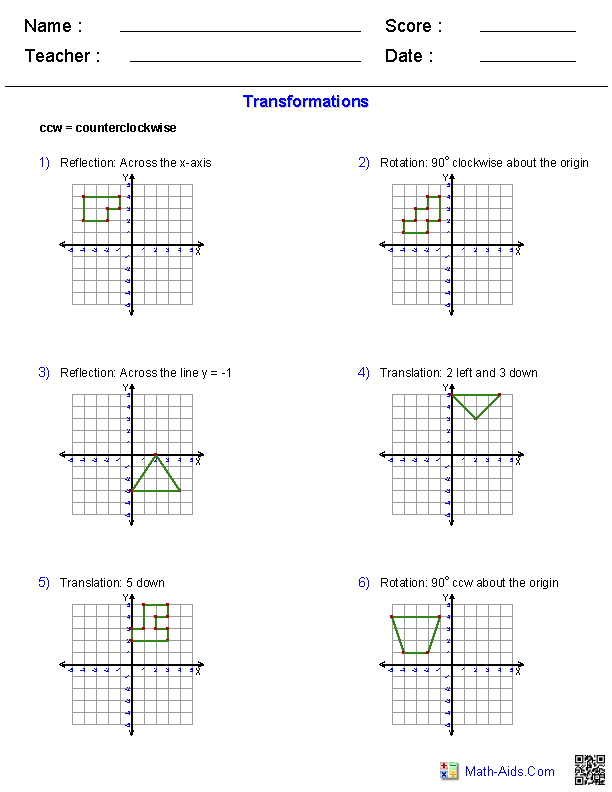
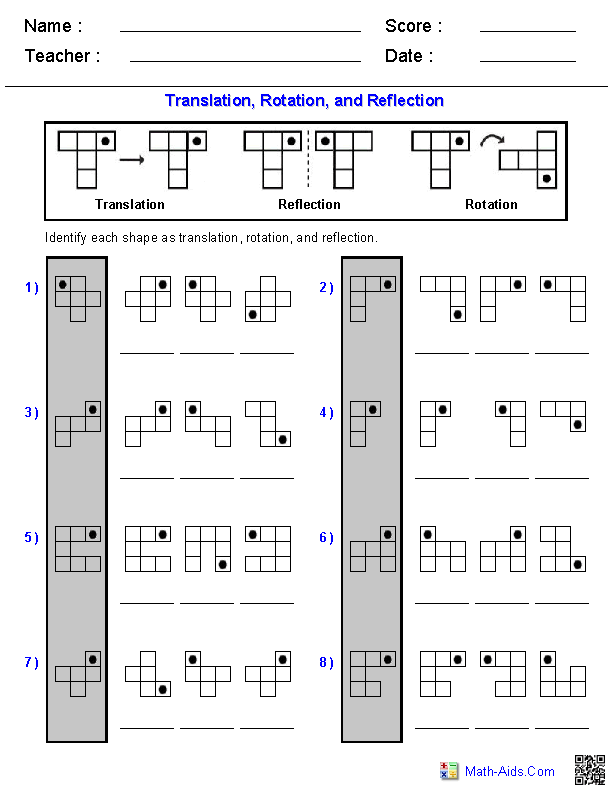
Here is a graphic preview for all of the Transformations Worksheets. You can select different variables to customize these Transformations Worksheets for your needs. The Transformations Worksheets are randomly created and will never repeat so you have an endless supply of quality Transformations Worksheets to use in the classroom or at home. We have classifying and naming Transformations, reading protractors and measuring Transformations, finding complementary, supplementary, verical, alternate, corresponding Transformations and much more. Our Transformations Worksheets are free to download, easy to use, and very flexible.
These Transformations Worksheets are a great resource for children in 3rd Grade, 4th Grade, 5th Grade, 6th Grade, 7th Grade, and 8th Grade.
Click here for a Detailed Description of all the Geometry Worksheets.